2026锦州国家公务员职位表在哪查询

　　辽宁华图_国家公务员考试为您提供2026年国家公务员考试文章：2026锦州国家公务员职位表在哪查询。更多2026年国家公务员招聘信息敬请关注辽宁国家公务员考试频道(http://ln.huatu.com/guojia/)或者关注辽宁华图微信公众号(syhuatu),辽宁华图咨询电话：400-024-1113。国家公务员考试专属客服:点击

　　辽宁华图小编为您整理国家公务员考试文章：2026锦州国家公务员职位表在哪查询

　　扫码领取历年国考各岗位报考统计分析、进面分数线、备考资料，向华图老师咨询如何选岗等考试信息

　　点击查看：2026年国家公务员考试公告>>>>(建议保存链接，出公告查看）

　　2026年国家公务员考试公告暂未发布，历年国家公务员考试公告都在10月中旬左右发布。

　　点击查看：2026年国家公务员考试职位表>>>>(建议保存链接，出职位表查看）

　　点击查看：2026年国家公务员考试大纲>>>>(建议保存链接，出大纲查看）

　　点击查看：2025年国家公务员考试公告>>>>

　　 2026年国家公务员笔试图书教材

　　2026年国家公务员面授笔试课程

　　2026年国家公务员精品网校课程

　　因篇幅有限，仅展示部分地市，完整版可扫码免费获取!

　　以上这些就是辽宁华图老师为大家分享的2026国家公务员考试文章：2026锦州国家公务员职位表在哪查询，期待大家继续关注同类话题的学习!

　　相关信息推荐：

　　2026辽宁国家公务员考试笔试课程

　　2026辽宁国家公务员考试面试课程

　　2026辽宁国家公务员考试试题资料、备考技巧

　　辽宁华图小编为您整理国考备考技巧

　　数量关系备考技巧：正整数范围内求解不定方程

　　在行测数量关系考查中出现不定方程时，多以日常生活事件作为出题背景，因此在这类题的求解过程中会出现一个隐含的条件就是所设未知数属于正整数范围，接下来华图教育就带大家一起学习在正整数范围内如何求解不定方程。

　　一、定义

　　不定方程：未知数个数多于独立方程个数的方程叫做不定方程。

　　例如：2x+y=10

　　二、在正整数范围内求解不定方程

　　方法一：整除法：当常数项与某一未知数系数有公约数时，用整除特性。

　　例题

　　例如：7x+6y=48.已知x，y为正整数，则x=( )

　　A.4

　　B.6

　　C.9

　　D.11

　　【华图解析】答案选B。6和48都能被6整除，故7x也能被6整除，即x能被6整除，结合选项，选B。

　　方法二：奇偶性：当两个未知数系数为一奇一偶时，考虑使用奇偶性。

　　例题

　　例如：x+2y=14.已知x，y为正整数且x为质数，则x=( )

　　A.2 B.3 C.4 D.5

　　【华图解析】答案选A。未知数系数一奇一偶，14是偶数，2y一定是偶数，故x也为偶数，又因为x为质数，所以x=2.选A。

　　方法三：尾数法：当某个未知数系数为5或5的倍数时，考虑使用尾数法。(常和奇偶性结合使用)

　　例题

　　例如：4x+5y=21.已知x，y为正整数，则x=( )

　　A.1

　　B.2

　　C.3

　　D.4

　　【华图解析】答案选D。未知数系数一奇一偶，21是奇数，4x一定是偶数，所以5y为奇数，故5y的尾数为5.又因21尾数为1.所以4x尾数为6.结合选项x=4.选D。

　　在正整数范围内求解不定方程时，若所设未知数为所求量，则可直接代入选项求解;若所求量需通过设未知数列方程间接求解，则可用上述总结的方法求解。

　　判断推理备考技巧：图形推理对称花式考法大全

　　当图形相异且相对规整时，我们可以考虑对称，对称的常见的考法有：

　　1.分类：轴对称图形，中心对称图形，既是轴对称又是中心对称图形

　　2.对称轴的方向

　　3.对称轴的条数

　　4对称轴过图形的线、点

　　5.对称轴的夹角

　　我们在做题的时候，可以尝试从这几个角度入手做题。我们一起来练习一下。如：

　　题目1

　　把下面的六个图形分为两类，使每一类图形都有共同特征或者规律，下面分类正确的一项是：

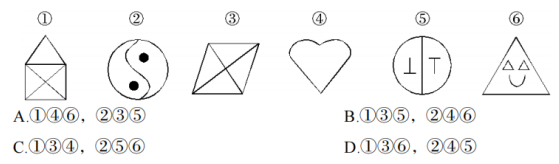
　　【答案】A。图形①④⑥均为竖直对称图形，图形②③⑤均为中心对称图形

　　题目2

　　从所给的四个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性：

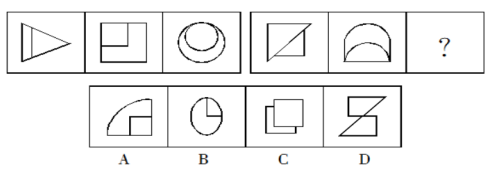
　　【答案】C。每组图形中，图形的对称轴依次顺时针旋转 45°，应选择一个对称轴与水平线呈 45°角的图形，只有 C 符合。

　　题目3

　　把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：

　　【答案】D。①②⑤图形都有三条对称轴;③④⑥图形都只有一条对称轴。

　　题目4

　　把下面的六个图形分为两类，使每一类图形都有各自的共同特征或规律，分类正确的一项是：

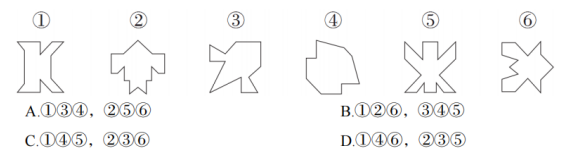
　　【答案】图形①④⑤的对称轴过图形的线，图形②③⑥的对称轴过图形的点。故本题选 C。

　　做行测图形推理题目的过程当中，大家对于同一规律的花式考法，要善于总结，扎实基本功，培养发散思维，做到事半功倍备考。

　　数量关系备考技巧：“容斥问题”怎么破

　　二者容斥即指集合A和集合B之间有交叉，文字这样说可能有点晦涩难懂，我们来看一个简单的例子。

　　例1

　　全班中，第一次参加文娱晚会的有 26 人，第二次参加文娱晚会的有 24 人，那可以知道全班人数吗?

　　【华图解析】不能，因为有人既参加第一次文娱晚会也参加第二次文娱晚会，还有人两次文娱晚会都不参加的。

　　那具体怎么求解呢?解决这类问题有两种方法，可以用公式法，也可以用图解法。

　　通过画图可推出二 集合容斥公式 为： A+B-A∩B+M=总数(I)，注M为两者都不满足数。接下来，我们再来实战一下。

　　例2

　　某单位组织党员进行党员知识考试，已知该单位的党员总数为32人，在第一次考试中有26人及格，在第二次考试中有24人及格，若两次考试中，都没及格的有4人，那么两次都及格的人数是( )。

　　A.12

　　B.18

　　C.22

　　D.27

　　【华图解析】答案选C。共有党员32人，即I=32.第一次有26人及格，即A=26.第二次考试有24人及格，即B=24.都没有及格的有4人，即M=4.求两次都及格的人数，即A∩B。应用公式I=A+B-A∩B+M即可得到，32=26+24-A∩B+4.解得A∩B=22.故选择C选项。

【国考笔试课程】|【国考面试课程】|【国考直播课程】|【国考备考资料】